题目内容
11.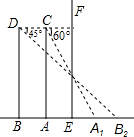 如图所示,细心的王聪站立在镜子EF前的A处时,此时他看自己的脚在镜中的像A1的俯角为60°;如果王聪向后退0.3米到B处,这时他看自己的脚在镜中的像B1的俯角为45°.求王聪的眼睛到地面的距离BD.(结果精确到0.01米,参考数据:$\sqrt{3}≈1.73$)
如图所示,细心的王聪站立在镜子EF前的A处时,此时他看自己的脚在镜中的像A1的俯角为60°;如果王聪向后退0.3米到B处,这时他看自己的脚在镜中的像B1的俯角为45°.求王聪的眼睛到地面的距离BD.(结果精确到0.01米,参考数据:$\sqrt{3}≈1.73$)
分析 根据平面镜的性质得出AB=0.3m,则A1B1=0.3m,设AE=xm,则A1E=xm,利用tan60°=$\frac{AC}{A{A}_{1}}$求出x的值,进而得出BD的值即可.
解答 解:由题意可得:AB=0.3m,则A1B1=0.3m,∠CA1A=∠FCA1=60°,
设AE=xm,则A1E=xm,
故BD=AC=2x+0.6,
则tan60°=$\frac{AC}{A{A}_{1}}$=$\frac{2x+0.6}{2x}$=$\sqrt{3}$,
解得:x=$\frac{3(\sqrt{3}+1)}{20}$≈0.41,
故BD=2x+0.6=1.42(m).
答:王聪的眼睛到地面的距离BD为1.42m.
点评 此题主要考查了解直角三角形的应用,正确利用平面镜的性质得出AE=A1E=x是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
6.函数y=$\frac{1-k}{x}$的图象与直线y=-x没有交点,那么k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k>-1 | D. | k<-1 |
16.某校为了解九年级11个班级学生(每班40名)的视力情况,下列做法中,比较合理的是( )
| A. | 了解每一名学生的视力情况 | |
| B. | 了解每一名男生的视力情况 | |
| C. | 了解每一名女生的视力情况 | |
| D. | 每班各抽取10名男生和10名女生,了解他们的视力情况 |
1.下列运算中,正确的是( )
| A. | 2x-x=1 | B. | x+x=2x | C. | (x3)3=x6 | D. | x8÷x2=x4 |
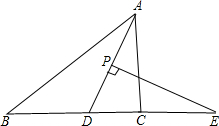 在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).
在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).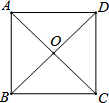 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点.