题目内容
8.在A,B,C,D四张卡片上分别用一句话描述了一个图形,依次为:A:内角和等于外角和的一半的正多边形;B:一个内角为108°的正多边形;
C:对角线互相平分且相等的四边形;D:每个外角都是36°的多边形.
(1)依次说出这四张卡片上描述的图形名称;
(2)从这四张卡片中任取两张,描述的图形都既是轴对称图形又是中心对称图形的概率是多少(利用树状图或列表来求解)?
分析 (1)根据正多边形的长性质以及矩形的判定方法逐项分析即可得到四张卡片上描述的图形名称;
(2)画出树状图,然后根据概率公式列式计算即可得解.
解答 解:(1)A:内角和等于外角和的一半的正多边形是等边三角形;
B:一个内角为108°的正多边形是正五边形;
C:对角线互相平分且相等的四边形是矩形;
D:每个外角都是36°的多边形不一定是正十边形;
(2)根据题意画出树状图如下: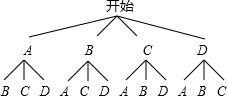
一共有12种情况,抽出的两张卡片的图形是既是轴对称图形又是中心对称图形的共有种情况,
所以既是轴对称图形又是中心对称图形的概率是$\frac{1}{12}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
16.某校为了解九年级11个班级学生(每班40名)的视力情况,下列做法中,比较合理的是( )
| A. | 了解每一名学生的视力情况 | |
| B. | 了解每一名男生的视力情况 | |
| C. | 了解每一名女生的视力情况 | |
| D. | 每班各抽取10名男生和10名女生,了解他们的视力情况 |
13.直线y=2x-2与x轴交于点A,与y轴交于点B,过点B作直线BP交x轴于点P,且OP=2OA,则△ABP的面积是( )
| A. | 1 | B. | 2 | C. | 1或3 | D. | 2或4 |
17.下列运算中,正确的是( )
| A. | -(m+n)=n-m | B. | (m2n2)3=m6n6 | C. | m3•m2=m6 | D. | n3÷n3=n |