题目内容
17.二次函数y=-5(x+m)2中.当x<-5时.y随x的增大而增大,当x>-5时.y随x的增大而减小,则m=5,此时,二次函数的图象的顶点坐标为(-5,0),当x=-5时,y取最大值,为0.分析 由二次函数的增减性可求得对称轴,则可求得m的值,容易求得其顶点坐标,则可求得其最大值.
解答 解:
∵y=-5(x+m)2,
∴抛物线开口向下,对称轴为x=-m
∵当x<-5时.y随x的增大而增大,当x>-5时,y随x的增大而减小,
∴抛物线对称轴为x=-5,
∴m=5,
∴抛物线解析式为y=-5(x+5)2,
∴抛物线顶点坐标为(-5,0),当x=-5时,y取最大值,最大值为0,
故答案为:5;(-5,0);-5;大;0.
点评 本题主要考查二次函数的性质,掌握抛物线的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.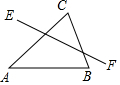 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )| A. | 4$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
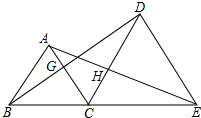 如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证:
如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证: