题目内容
6.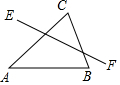 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )| A. | 4$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 先连接CD,CE,CF,根据点D关于AC,BC对称点分别是点E和点F,得出△CEF是等腰三角形,再根据∠A=45°,∠B=75°,求得∠ACB=60°,∠ECF=120°,∠CEF=∠CFE=30°,根据垂线段最短求得CD的长,最后过点C作CG⊥EF,在等腰三角形ECF中,根据EF=2EG,求得EF.
解答 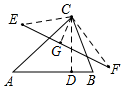 解:如图,连接CD,CE,CF,
解:如图,连接CD,CE,CF,
∵点D关于AC,BC对称点分别是点E和点F,
∴CE=CD=CF,∠ACB=$\frac{1}{2}$∠ECF,
∴△CEF是等腰三角形,
∵∠A=45°,∠B=75°,
∴∠ACB=60°,
∴∠ECF=120°,∠CEF=∠CFE=30°,
∴当CE,CF最短时,EF最短,
∵当CD⊥AB时,CD最短,而AC=8,
∴Rt△ACD中,CD=4$\sqrt{2}$,
∴CE=CD=CF=4$\sqrt{2}$,
过点C作CG⊥EF,则等腰三角形ECF中,EF=2EG,
∵Rt△CEG中,CG=$\frac{1}{2}$CE=2$\sqrt{2}$,
∴EG=2$\sqrt{6}$,
∴EF=2EG=4$\sqrt{6}$.
故选:A.
点评 本题主要考查了轴对称的性质,等腰三角形的性质,以及含30°角的直角三角形的性质的综合应用,解决问题的关键是作辅助线构造等腰三角形和直角三角形,根据垂线段最短进行判断.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
14.已知$\sqrt{x}$=$\frac{1-a}{2}$,$\sqrt{x+a}$-$\sqrt{x-a+2}$=-2,则a的取值范围是( )
| A. | a≤1 | B. | -1≤a≤1 | C. | a≤-1 | D. | -1≤a≤0 |
7.要使△ABC≌△A′B′C′,需要满足的条件是( )
| A. | AB=A′B′,∠B=∠B′,AC=A′C′ | B. | AB=A′B′,∠A=∠A′,BC=B′C′ | ||
| C. | AC=A′C′,∠C=∠C′,BC=B′C′ | D. | AC=A′C′,∠B=∠B′,BC=B′C′ |
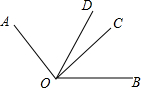 如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.
如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.