题目内容
9.不改变分式的值,使分式$\frac{1-{a}^{3}-{a}^{2}}{1+{a}^{4}-{a}^{2}}$中分子、分母最高次项的系数为正,则正确的结果为-$\frac{{a}^{3}+{a}^{2}-1}{{a}^{4}-{a}^{2}+1}$.分析 利用分式的基本性质变形即可得到结果.
解答 解:原式=-$\frac{{a}^{3}+{a}^{2}-1}{{a}^{4}-{a}^{2}+1}$,
故答案为:-$\frac{{a}^{3}+{a}^{2}-1}{{a}^{4}-{a}^{2}+1}$
点评 此题考查了分式的基本性质,熟练掌握分式的基本性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.如果一个单项式与-3ab的积为-$\frac{3}{4}$a2bc,则这个单项式为( )
| A. | $\frac{1}{4}$ a2c | B. | $\frac{1}{4}$ ac | C. | $\frac{9}{4}$ a2c | D. | $\frac{9}{4}$ ac |
20.$\frac{x-1}{{x}^{2}+x-6}$,$\frac{2}{{x}^{2}-9}$,$\frac{x-2}{{x}^{2}+5x+6}$的最简公分母是( )
| A. | (x+3)2(x+2)(x-2) | B. | (x2-9)2(x2-4) | C. | (x2-9)2(x-4)2 | D. | (x+3)2(x-3)2(x2+2)(x-2) |
14.已知$\sqrt{x}$=$\frac{1-a}{2}$,$\sqrt{x+a}$-$\sqrt{x-a+2}$=-2,则a的取值范围是( )
| A. | a≤1 | B. | -1≤a≤1 | C. | a≤-1 | D. | -1≤a≤0 |
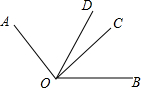 如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.
如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.