题目内容
20. 如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.
如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.解:因为∠1=∠2(已知),
所以AD∥BC(内错角相等,两直线平行),
得∠ABC+∠A=180°(两直线平行,同旁内角互补).
因为∠ABC=31°(已知),
所以∠A=180°-∠ABC=149°(等式性质).
分析 根据内错角相等,两直线平行,得到AD∥BC,再根据平行线的性质,即可得到∠ABC+∠A=180°,进而得出∠A的度数.
解答 解:因为∠1=∠2(已知),
所以AD∥BC(内错角相等,两直线平行),
得∠ABC+∠A=180°(两直线平行,同旁内角互补).
因为∠ABC=31°(已知),
所以∠A=180°-∠ABC=149°(等式性质).
故答案为:AD∥BC,内错角相等,两直线平行;∠ABC+∠A=180°,两直线平行,同旁内角互补;ABC,149.
点评 本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
相关题目
10.计算:$\sqrt{80}$+[$\sqrt{12}$+$\sqrt{20}$-($\sqrt{5}$-$\sqrt{3}$)-$\sqrt{45}$]( )
| A. | 2$\sqrt{3}$+$\sqrt{5}$ | B. | 2$\sqrt{3}$+2$\sqrt{5}$ | C. | 3$\sqrt{3}$+2$\sqrt{5}$ | D. | 3$\sqrt{3}$+$\sqrt{5}$ |
8.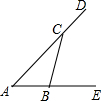 如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
 如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )
如图,B、C两点在线段AE、AD上,若在线段BC上求一点P,使点P到AD,AE的距离相等,则P点是( )| A. | 线段BC的中点 | B. | AE的垂直平分线与线段BC的交点 | ||
| C. | AC的垂直平分线与线段BC的交点 | D. | ∠CAB的平分线与BC的交点 |
 下面是两个由边长为1的小正方形组成的4×4的正方形网格,请只用无刻度的直尺在网格中各画一个有一条直角边长为$\sqrt{5}$的直角三角形.
下面是两个由边长为1的小正方形组成的4×4的正方形网格,请只用无刻度的直尺在网格中各画一个有一条直角边长为$\sqrt{5}$的直角三角形.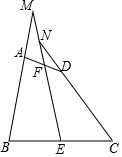 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.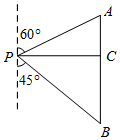 如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.