题目内容
10.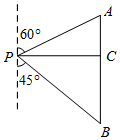 如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
分析 由已知可得△ABP中∠A=60°∠B=45°且PC=60m,要求AB的长,可以先求出AC和BC的长就可转化为运用三角函数解直角三角形.
解答  解:由题意可知:
解:由题意可知:
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△BPC中,
∵∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
tan30°=$\frac{AC}{PC}$,
∴AC=PC•tan30°=tan30°×60=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$(米).
∴AB=AC+BC=60+20$\sqrt{3}$(米).
答:教学楼A与办公楼B之间的距离是(60+20$\sqrt{3}$)米.
故答案是:(60+20$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用--方向角问题.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5.如果把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
19.四边形ABCD中,AC=BD,顺次连接ABCD各边中点得到的图形为( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
 如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.
如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.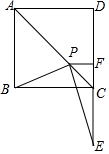 在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.
在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.



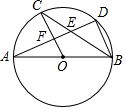 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.