题目内容
15.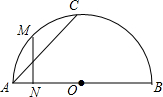 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
分析 连接OM、OC,交AC于D,根据圆心角、弧、弦的关系证得∠AOM=∠COM,进而根据等腰三角形的性质得出OM⊥AC,AD=CD=$\frac{1}{2}$AC,求得∠A=∠OMN,根据余弦函数得出$\frac{AD}{OA}$=$\frac{MN}{OM}$,进而等量代换即可证得MN=$\frac{1}{2}$AC.
解答  解:连接OM、OC,交AC于D,
解:连接OM、OC,交AC于D,
∵M是弧AC的中点,
∴∠AOM=∠COM,
∵OA=OC,
∴OM⊥AC,AD=CD=$\frac{1}{2}$AC,
∴∠A+∠AOM=90°,
∵MN⊥AB,
∴∠OMN+∠AOM=90°,
∴∠A=∠OMN,
∴cos∠A=cos∠OMN,
∴$\frac{AD}{OA}$=$\frac{MN}{OM}$,
∵OA=OM,AD=$\frac{1}{2}$AC,
∴$\frac{\frac{1}{2}AC}{OA}$=$\frac{MN}{OA}$,
∴MN=$\frac{1}{2}$AC.
故选A.
点评 本题考查了圆心角、弧、弦的关系,等腰三角形的性质,直角三角函数等,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
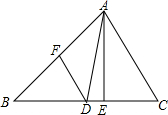 如图,△ABC中,AE⊥BC于点E,AD为BC边上的中线,DF为△ABD中AB边上的中线,已知AB=5cm,AC=3cm,△ABC的面积为12cm2.
如图,△ABC中,AE⊥BC于点E,AD为BC边上的中线,DF为△ABD中AB边上的中线,已知AB=5cm,AC=3cm,△ABC的面积为12cm2.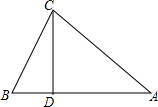 已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm
已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm  已知:如图,∠1和线段m,n.
已知:如图,∠1和线段m,n.