题目内容
3.已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是最小的正整数,求m+$\frac{2007(a+b)}{2008}$-cd的值为0.分析 a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是最小的正整数,可分别求得a+b=0,cd=1,m=1,代入求值即可.
解答 解:因为a、b互为相反数且a≠0,
所以a+b=0,
又因为c、d互为倒数,m的绝对值是最小的正整数,
所以cd=1,m=1,
所以m+$\frac{2007(a+b)}{2008}$-cd=1+0-1=0.
故答案为:0.
点评 本题考查代数式求值,掌握倒数、相反数、绝对值的有关概是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.填表:
| 多边形的边数 | 7 | 17 | 20 | 25 |
| 内角和 | 5×180° | 15×180° | 18×180° | 23×180° |
| 外角和 | 360° | 360° | 360° | 360° |
15.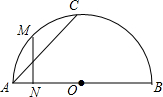 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
 如图所示,点D是等边三角形ABC内一点,以CD为一边且在CD下方作等边三角形CDE,连接AD,BE,求证:△ACD≌△BCE.
如图所示,点D是等边三角形ABC内一点,以CD为一边且在CD下方作等边三角形CDE,连接AD,BE,求证:△ACD≌△BCE.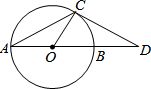 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.