题目内容
6.根据绝对值的意义,对于有理数a有,当a>0时,|a|=a(一个正数的绝对值是它本身);当a=0时,|a|=0(零的绝对值是零);当a<0时,|a|=-a(一个负数的绝对值是它的相反数).即|a|=$\left\{\begin{array}{l}a(a>0)\\ 0(a=0)\\-a(a<0)\end{array}$
请你仿此写出下列各有理数的绝对值:
①|a-1|,②|a-b|,③|m+4|.
分析 类比给出的方法,根据字母的取值范围得出结果即可.
解答 解:①|a-1|=$\left\{\begin{array}{l}{a-1(a>1)}\\{0(a=1)}\\{1-a(a<1)}\end{array}\right.$;
②|a-b|=$\left\{\begin{array}{l}{a-b(a>b)}\\{0(a=b)}\\{b-a(a<b)}\end{array}\right.$;
③|m+4|=$\left\{\begin{array}{l}{m+4(m>-4)}\\{0(m=-4)}\\{-m-4(m<-4)}\end{array}\right.$.
点评 此题考查绝对值的意义与性质,理解绝对值的意义,根据字母的不同取值范围化简即可.

练习册系列答案
相关题目
15.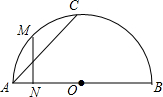 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
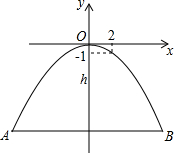 如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.
如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.