题目内容
10.已知a、b、c、d是成比例线段.(1)若a=4,b=1,c=12,求d.
(2)若a=1.5,b=2.5,d=2,求c.
分析 由a、b、c、d是成比例线段,得出a:b=c:d,根据比例的基本性质得到ad=bc,再将已知条件代入即可求解(1)(2).
解答 解:∵a、b、c、d是成比例线段,
∴a:b=c:d,
∴ad=bc.
(1)∵a=4,b=1,c=12,
∴4d=1×12,
∴d=3;
(2)∵a=1.5,b=2.5,d=2,
∴1.5×2=2.5c,
∴c=1.2.
点评 本题考查了比例线段,关键是理解比例线段的概念,列出比例式,用到的知识点是比例的基本性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知a=$\frac{\sqrt{5}+2}{\sqrt{5}-2}$,b=$\frac{\sqrt{5}-2}{\sqrt{5}+2}$,求$\sqrt{\frac{a+b}{ab}}$的值.
15.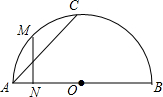 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
2.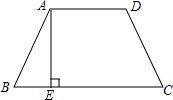 如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
 如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )| A. | 8,9$\sqrt{3}$ | B. | 10$\sqrt{3}$,9$\sqrt{3}$ | C. | 9$\sqrt{3}$,10$\sqrt{3}$ | D. | 8$\sqrt{3}$,9$\sqrt{3}$ |
19.$-4{x^4}{y^2}{z^2}÷(-\frac{1}{2}{x^3}yz)$的结果是( )
| A. | 8xyz | B. | -8xyz | C. | 2xyz | D. | 8xy2z2 |
