题目内容
4.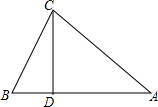 已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm
已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm (1)求CD的长;
(2)求AB的长;
(3)△ABC是否为直角三角形?请说明理由.
分析 (1)在Rt△ACD中运用勾股定理即可求出CD的长;
(2)先在Rt△BCD中运用勾股定理求出BD的长,再根据AB=BD+AD即可求解;
(3)已知△ABC的三边,根据勾股定理的逆定理即可判定△ABC是直角三角形.
解答 解:(1)在Rt△ACD中,∵∠CDA=90°,AC=$\sqrt{34}$cm,AD=5cm,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=3cm;
(2)在Rt△BCD中,∵∠CDB=90°,BC=$\sqrt{10}$cm,CD=3cm,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=1cm,
∴AB=BD+AD=6cm;
(3)在△ABC中,∵AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AB=6cm,
∴AC2+BC2=34+10=44≠36=AB2,
∴△ABC不是直角三角形.
点评 本题考查了勾股定理及其逆定理,比较简单.用到的知识点:
勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
15.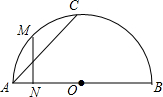 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
19.$-4{x^4}{y^2}{z^2}÷(-\frac{1}{2}{x^3}yz)$的结果是( )
| A. | 8xyz | B. | -8xyz | C. | 2xyz | D. | 8xy2z2 |
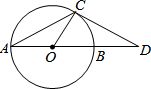 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
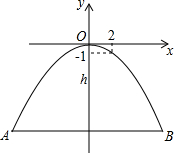 如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.
如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.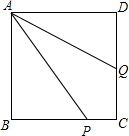 ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.
ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.