题目内容
7.先化简,再求值:$\frac{1}{{m}^{2}+6m+9}$•(m+2+$\frac{5}{2-m}$)÷$\frac{3-m}{{m}^{2}-4}$,其中m=2.分析 首先计算括号里面的通分,再计算乘除,首先把分子分母分解因式,然后约分,化简后再代入m的值计算即可.
解答 解:原式=$\frac{1}{(m+3)^{2}}$$•\frac{4-{m}^{2}+5}{2-m}$÷$\frac{3-m}{{m}^{2}-4}$,
=$\frac{1}{(m+3)^{2}}$•$\frac{(3+m)(3-m)}{2-m}$•$\frac{(m+2)(m-2)}{3-m}$,
=-$\frac{m+2}{m+3}$
当m=2时,
原式=-$\frac{2+2}{2+3}$=-$\frac{4}{5}$.
点评 此题主要考查了分式的化简求值,关键是掌握在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2.当a>0时,下列关于幂的运算正确的是( )
| A. | a0=0 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a-2=$\frac{1}{{a}^{2}}$ |
16.如图,过点P画出直线AB的垂线.下列画法中,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
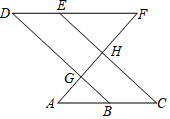 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.
如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.