题目内容
17.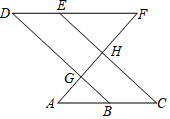 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.
如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.证明:∵∠AGB=∠EHF(理由:已知)
∠AGB=∠DGF(对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由:同位角相等,两直线平行)
∴∠C=∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥AC(内错角相等,两直线平行)
∴∠A=∠F(理由:两直线平行,内错角相等).
分析 根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
解答 解:∵∠AGB=∠EHF(已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA ( 两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案是:已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等.
点评 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
9.将一元一次方程$\frac{x}{3}$-5=$\frac{x-1}{2}$去分母后,正确的是( )
| A. | x-5=x-1 | B. | 2x-5=3x-1 | C. | 2x-30=3x-3 | D. | 2x-30=3x-1 |
7.下列图中不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
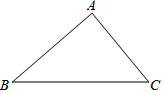 已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.
已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.