题目内容
17.李华老师给学生出了一道题:当a=0.35,b=-0.28时,求7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+3的值,题目出完后,小明说:“老师给的条件a=0.35,b=-0.28是多余的.”王光说:“不给这两个条件,就不能求出结果,所以不是多余的.”你认为他们谁说的有道理?为什么?分析 先合并同类项,根据求出的结果判断即可.
解答 解:小明说的有道理,
理由是:7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+3
=(7a3+3a3-10a3)+(6a3b-6a3b)+(3a2b-3a2b)+3
=3,
即无论a、b为何值,代数式的值恒为3,
所以小明的说法是正确的.
点评 本题考查了整式的加减,能正确根据整式的加减法则进行计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.小明根据华师版八年级下册教材P37学习内容,对函数y=$\frac{1}{2}$x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
其中n=-3;
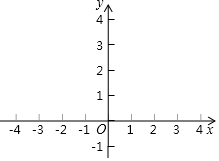
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
| x | … | -4 | n | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.

12. 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 60° |
2.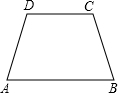 如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
 如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )| A. | 6$\sqrt{15}$ | B. | 12$\sqrt{15}$ | C. | 6$\sqrt{17}$ | D. | 6$\sqrt{5}$ |
6.已知a+$\frac{1}{a}$=$\sqrt{10}$,则a-$\frac{1}{a}$的值为( )
| A. | 2 | B. | 6 | C. | ±$\sqrt{6}$ | D. | ±2$\sqrt{2}$ |

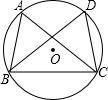 如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.
如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.