题目内容
18. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{4π}{3}$ | B. | $\sqrt{3}$,π | C. | 2$\sqrt{3}$,$\frac{8π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
分析 连接OC、OB,证出△BOC是等边三角形,根据锐角三角函数的定义求出OM,再由弧长公式求出弧BC的长即可.
解答 解:如图所示,连接OC、OB,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OA=OB,
∴△BOC是等边三角形,
∴∠OBM=60°,
∴OM=OBsin∠OBM=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
$\widehat{BC}$的长=$\frac{60π×4}{180}$=$\frac{4π}{3}$;
故选:D.
点评 本题考查的是正六边形的性质、等边三角形的判定与性质、三角函数;熟练掌握正六边形的性质,由三角函数求出OM是解决问题的关键.

练习册系列答案
相关题目
8.在Rt△ABC中,若各边长都扩大3倍,则锐角A的正弦值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小到原来的$\frac{1}{3}$ | D. | 不能确定 |
6.方程(x-1)(x+2)=x-1的解是( )
| A. | -2 | B. | 1,-2 | C. | -1,1 | D. | -1,3 |
13.下列说法错误的是( )
| A. | 四边形的内角和与外角和相等 | |
| B. | 五边形的每一个内角都是108° | |
| C. | 六边形的内角和等于其外角和的2倍 | |
| D. | 从n边形的一个顶点出发可以引(n-3)条对角线 |
3. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-2 | C. | x<-1 | D. | 无法确定 |
10.如果不等式组$\left\{\begin{array}{l}{x+7<3x-7}\\{x>n}\end{array}\right.$的解集是x>7,则n的取值范围是( )
| A. | n=7 | B. | n<7 | C. | n≥7 | D. | n≤7 |
7.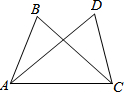 如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
 如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )| A. | BC=AD | B. | ∠B=∠D=90° | C. | ∠BAC=∠CAD | D. | ∠ACB=∠CAD |
8. 12月4日是国家“宪法日”,某地区随机抽取了一部分市民进行了宪法知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制频数直方图如图所示,下列说法不正确的是( )
12月4日是国家“宪法日”,某地区随机抽取了一部分市民进行了宪法知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制频数直方图如图所示,下列说法不正确的是( )
 12月4日是国家“宪法日”,某地区随机抽取了一部分市民进行了宪法知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制频数直方图如图所示,下列说法不正确的是( )
12月4日是国家“宪法日”,某地区随机抽取了一部分市民进行了宪法知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制频数直方图如图所示,下列说法不正确的是( )| A. | 由6人成绩为100分 | |
| B. | 测试成绩在70-80分的人数最多 | |
| C. | 这次活动共抽调了48人测试 | |
| D. | 若成绩在80分以上(含80分)为优秀,则优秀率为31.25% |