题目内容
7.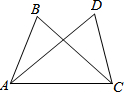 如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )| A. | BC=AD | B. | ∠B=∠D=90° | C. | ∠BAC=∠CAD | D. | ∠ACB=∠CAD |
分析 全等三角形的判定定理有SAS,ASA,AAS,SSS(直角三角形还有HL),看看是否符合定理,即可判断选项.
解答 解:A、∵在△ABC和△CDA中
$\left\{\begin{array}{l}{AC=CA}\\{AB=CD}\\{BC=AD}\end{array}\right.$
∴△ABC≌△CDA(SSS),正确,故本选项不符合题意;
B、∵∠B=∠D=90°,
∴在Rt△ABC和Rt△CDA中
$\left\{\begin{array}{l}{AC=CA}\\{AB=CD}\end{array}\right.$
∴Rt△ABC≌Rt△CDA(HL),正确,故本选项不符合题意;
C、根据AB=CD,AC=AC,∠BAC=∠CAD不能推出△ABC≌△CDA,错误,故本选项符合题意;
D、∵在△ABC和△CDA中
$\left\{\begin{array}{l}{AB=CD}\\{∠BAC=∠DCA}\\{AC=CA}\end{array}\right.$
∴△ABC≌△CDA(SAS),正确,故本选项不符合题意;
故选:C.
点评 本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS(直角三角形还有HL).

练习册系列答案
相关题目
17.已知关于x的方程(a-1)x|a|+1-2x-1=0是一元二次方程,则a的值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 1或-1 |
18. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{4π}{3}$ | B. | $\sqrt{3}$,π | C. | 2$\sqrt{3}$,$\frac{8π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
15.已知点A(-1,-2),B关于抛物线y=a(x-1)2的对称轴对称,则点B的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (2,-2) | D. | (3,-2) |
2. 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{17}$ |
12.必然事件的概率是( )
| A. | 1 | B. | 0 | C. | 大于0且小于1 | D. | 大于1 |
17.若|n+2|+|m+8|=0,则n-m等于( )
| A. | 6 | B. | -10 | C. | -6 | D. | 10 |