题目内容
6．方程（x-1）（x+2）=x-1的解是（ ）| A． | -2 | B． | 1，-2 | C． | -1，1 | D． | -1，3 |
分析 移项后分解因式，即可得出两个一元一次方程，求出方程的解即可．
解答 解：移项得：（x-1）（x+2）-（x-1）=0，
（x-1）[（x+2）-1]=0，
x-1=0，x+2-1=0，
x=1或-1，
故选C．
点评 本题考查了解一元二次方程，能把一元二次方程转化成一元一次方程是解此题的关键．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
17．已知关于x的方程（a-1）x|a|+1-2x-1=0是一元二次方程，则a的值为（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | 1或-1 |
14．
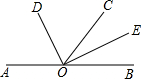如图，O是直线AB上的一点，过点O作射线OC，OD平分∠AOC，OE平分∠BOC，若∠DOC=50°，则∠BOE的度数为（ ）
如图，O是直线AB上的一点，过点O作射线OC，OD平分∠AOC，OE平分∠BOC，若∠DOC=50°，则∠BOE的度数为（ ）| A． | 50° | B． | 40° | C． | 25° | D． | 20° |
1．下列命题：①无理数都是无限小数；②$\sqrt{16}$的平方根是±4；③等腰三角形的对称轴是它顶角的平分线；④三角形三边垂直平分线的交点一定在这个三角形的内部，正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．若分式$\frac{1}{x（x+1）}$有意义，则x满足的条件是（ ）
| A． | x≠0 | B． | x≠1 | C． | x≠-1 | D． | x≠0，x≠-1 |
18．
如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）
如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）| A． | 2，$\frac{4π}{3}$ | B． | $\sqrt{3}$，π | C． | 2$\sqrt{3}$，$\frac{8π}{3}$ | D． | 2$\sqrt{3}$，$\frac{4π}{3}$ |
15．已知点A（-1，-2），B关于抛物线y=a（x-1）2的对称轴对称，则点B的坐标为（ ）
| A． | （1，-2） | B． | （-1，2） | C． | （2，-2） | D． | （3，-2） |