题目内容
9．已知$\frac{x+y}{y}$=3，则$\frac{x}{y}$=2．分析 根据比例的合比性质即可求解．
解答 解：∵$\frac{x+y}{y}$=3，
∴$\frac{x}{y}$=3-1=2．
故答案为：2．
点评 此题考查了比例的合比性质：若$\frac{a}{b}$=$\frac{c}{d}$，则$\frac{a+b}{b}$=$\frac{c+d}{d}$．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．
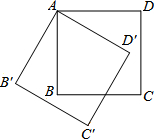如图，将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置，旋转角为30°，则C点运动到C′点的路径长为（ ）
如图，将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置，旋转角为30°，则C点运动到C′点的路径长为（ ）| A． | $\frac{2}{3}$πcm | B． | $\frac{2\sqrt{2}}{3}$πm | C． | $\frac{2\sqrt{3}}{3}$cm | D． | $\frac{2\sqrt{5}}{3}$cm |
20．若双曲线y=$\frac{1-k}{x}$的图象在第一、三象限，则k的取值范围为（ ）
| A． | k＞0 | B． | k＜0 | C． | k＞1 | D． | k＜1 |
17．已知关于x的方程（a-1）x|a|+1-2x-1=0是一元二次方程，则a的值为（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | 1或-1 |
4．
如图，在等腰△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合，则∠CEF的度数是（ ）
如图，在等腰△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合，则∠CEF的度数是（ ）| A． | 60° | B． | 55° | C． | 50° | D． | 45° |
14．
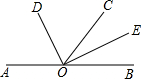如图，O是直线AB上的一点，过点O作射线OC，OD平分∠AOC，OE平分∠BOC，若∠DOC=50°，则∠BOE的度数为（ ）
如图，O是直线AB上的一点，过点O作射线OC，OD平分∠AOC，OE平分∠BOC，若∠DOC=50°，则∠BOE的度数为（ ）| A． | 50° | B． | 40° | C． | 25° | D． | 20° |
1．下列命题：①无理数都是无限小数；②$\sqrt{16}$的平方根是±4；③等腰三角形的对称轴是它顶角的平分线；④三角形三边垂直平分线的交点一定在这个三角形的内部，正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
18．
如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）
如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）| A． | 2，$\frac{4π}{3}$ | B． | $\sqrt{3}$，π | C． | 2$\sqrt{3}$，$\frac{8π}{3}$ | D． | 2$\sqrt{3}$，$\frac{4π}{3}$ |