题目内容
8.在Rt△ABC中,若各边长都扩大3倍,则锐角A的正弦值( )| A. | 不变 | B. | 扩大3倍 | C. | 缩小到原来的$\frac{1}{3}$ | D. | 不能确定 |
分析 设Rt△ABC的三边长为a,b,c,则sinA=$\frac{a}{c}$,如果各边长都扩大3倍,则sinA=$\frac{3a}{3c}$=$\frac{a}{c}$,得到答案.
解答 解:设Rt△ABC的三边长为a,b,c,则sinA=$\frac{a}{c}$,
如果各边长都扩大3倍,
∴sinA=$\frac{3a}{3c}$=$\frac{a}{c}$,
故∠A的正弦值大小不变.
故选:A.
点评 本题考查的是锐角三角函数的定义,掌握锐角A的对边a与斜边c的比叫做∠A的正弦是解题的关键.

练习册系列答案
相关题目
19.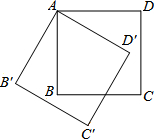 如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
 如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )| A. | $\frac{2}{3}$πcm | B. | $\frac{2\sqrt{2}}{3}$πm | C. | $\frac{2\sqrt{3}}{3}$cm | D. | $\frac{2\sqrt{5}}{3}$cm |
3.下列方程中,解为x=2的方程是( )
| A. | x+2=0 | B. | 2+3x=8 | C. | 3x-1=2 | D. | 4-2x=1 |
13.下列命题中,错误的是( )
| A. | 矩形的对角线互相平分且相等 | B. | 对角线互相垂直的矩形是正方形 | ||
| C. | 等腰梯形同一底上的两个角相等 | D. | 对角线互相垂直的四边形是菱形 |
20.若双曲线y=$\frac{1-k}{x}$的图象在第一、三象限,则k的取值范围为( )
| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
17.已知关于x的方程(a-1)x|a|+1-2x-1=0是一元二次方程,则a的值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 1或-1 |
18. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{4π}{3}$ | B. | $\sqrt{3}$,π | C. | 2$\sqrt{3}$,$\frac{8π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
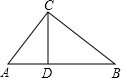 红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?