题目内容
5.已知一次函数y=-2x+6的图象与x轴、y轴分别相交于A、B两点,点C坐标(2,0),点D在直线y=-2x+6上,△OCD的面积是△AOB的面积的$\frac{1}{4}$,则点D的坐标为($\frac{15}{8}$,-$\frac{9}{4}$)或($\frac{33}{8}$,-$\frac{9}{4}$).分析 先求出A、B两点的坐标,设D(x,-2x+6),再由三角形的面积公式即可得出结论.
解答 解:∵一次函数y=-2x+6的图象与x轴、y轴分别相交于A、B两点,
∴A(3,0),B(0,6),
∴S△AOB=$\frac{1}{2}$×3×6=9.
设D(x,-2x+6),
∵点C坐标(2,0),
∴S△OCD=$\frac{1}{2}$×2|-2x+6|=|-2x+6|.
∵,△OCD的面积是△AOB的面积的$\frac{1}{4}$,
∴|-2x+6|=$\frac{9}{4}$,解得x=$\frac{15}{8}$或$\frac{33}{8}$,
∴D($\frac{15}{8}$,-$\frac{9}{4}$)或($\frac{33}{8}$,-$\frac{9}{4}$).
故答案为:($\frac{15}{8}$,-$\frac{9}{4}$)或($\frac{33}{8}$,-$\frac{9}{4}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
13.下表是一文具店1~7月份数学作业本销售情况统计表:
观察表中数据可知,众数是200,中位数是300.
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 作业本/本 | 300 | 200 | 400 | 500 | 300 | 200 | 200 |
14.平行四边形的两条对角线长分别为8cm和10cm,则其边长的范围是( )
| A. | 2<x<6 | B. | 3<x<9 | C. | 1<x<9 | D. | 2<x<8 |
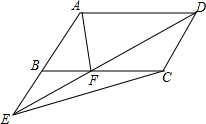 如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.