题目内容
15.计算或化简:(1)$\frac{2x}{x-y}+\frac{2y}{y-x}$;
(2)$\frac{{{x^2}-4}}{{{x^2}+2x+1}}÷({x+2})•\frac{x+1}{2-x}$.
分析 (1)先变号把分母化为同分母,再进行同分母的减法运算,然后约分即可;
(2)先把分子分母因式分解,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=$\frac{2x}{x-y}$-$\frac{2y}{x-y}$
=$\frac{2(x-y)}{x-y}$
=2;
(2)原式=$\frac{(x+2)(x-2)}{(x+1)^{2}}$•$\frac{1}{x+2}$•(-$\frac{x+1}{x-2}$)
=-$\frac{1}{x+1}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
5.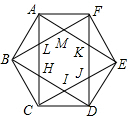 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )| A. | 18$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{18\sqrt{3}}{2}$ |
3.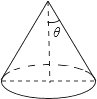 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
20.一个边长为a的正方形,若将其边长增加6cm,则新的正方形的面积增加( )
| A. | 36cm2 | B. | 12acm2 | C. | (36+12a)cm2 | D. | 以上都不对 |
7.已知x+y=6,xy=4,则x2y+xy2的值为( )
| A. | 12 | B. | -12 | C. | -24 | D. | 24 |