题目内容
19.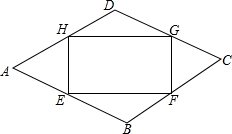 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.(1)求∠HEF的度数;
(2)判断四边形EFGH的形状,并说明理由;
(3)若AB=6,设AE=x,当x为何值时,四边形EFGH的面积最大?
分析 (1)根据菱形ABCD的性质和∠A=60°得出∠D=120°,从而得出∠HEF的度数;
(2)利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGF=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,即可证得;
(3)利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
解答 解:(1)∵四边形ABCD为菱形,
∴AB=BC=CD=AD,
∵BE=BF=DG=DH,
∴AE=AH,
∵∠A=60°,
∴△AEH为等边三角形,
∴∠AEH=60°,∠BEF=30°,
∴∠HEF=90°;
(2)证明:∵DG=DH,
∴∠DHG=∠DGH=30°,
同理,∠CGF=60°,
∴∠DGH+∠CGF=90°,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(3)∵AB=6,∠A=60°,AE=x,
∴EH=x,
则EF=$\sqrt{3}$(6-x),
则矩形EFGH的面积S=EH•EF=x•$\sqrt{3}$(6-x)=-$\sqrt{3}$x2+6$\sqrt{3}$x,
则当x=-$\frac{b}{2a}$=-$\frac{6\sqrt{3}}{-2\sqrt{3}}$=3时,函数有最大值.
∴当x为3时,四边形EFGH的面积最大.
点评 本题考查了菱形的性质,矩形的判定以及二次函数的性质,正确利用x表示出矩形EFGH的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.能判断平行四边形是菱形的条件是( )
| A. | 一个角是直角 | B. | 对角线相等 | C. | 一组邻角相等 | D. | 对角线互相垂直 |
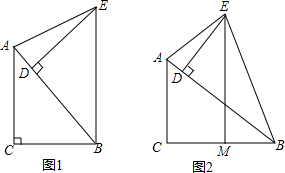
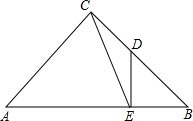 如图,已知△ABC是等腰直角三角形,∠ACB=90°,过BC的中点D作DE⊥AB于E,连结CE,求sin∠ACE=$\frac{3\sqrt{10}}{10}$.
如图,已知△ABC是等腰直角三角形,∠ACB=90°,过BC的中点D作DE⊥AB于E,连结CE,求sin∠ACE=$\frac{3\sqrt{10}}{10}$.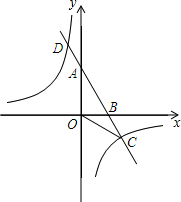 如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).
如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a). 如图,AC平分∠DAB,∠1=∠2,请结合图形填空:
如图,AC平分∠DAB,∠1=∠2,请结合图形填空: