题目内容
11.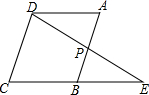 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.
分析 由平行四边形的性质和已知条件易证△ADP≌△BEP,进而可得BE=AD.
解答 证明:
∵四边形ABCD是平行四边形,
∴AD∥CE,
∴∠DAP=∠EBP,
∵点P是AB的中点,
∴AP=BP,
在△ADP和△BEP中
$\left\{\begin{array}{l}{∠DAP=∠EBP}\\{∠APD=∠BPE}\\{AP=BP}\end{array}\right.$,
∴△ADP≌△BEP(AAS),
∴BE=AD.
点评 本题考查的是利用平行四边形的性质结合三角形全等来解决有关线段相等的证明,是中考常见题型,比较简单.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19. 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )
 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | AC=BD | C. | AB=AD | D. | AO=CO |
16.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
20.能判断平行四边形是菱形的条件是( )
| A. | 一个角是直角 | B. | 对角线相等 | C. | 一组邻角相等 | D. | 对角线互相垂直 |
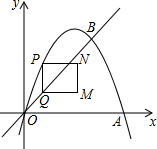 如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2). 已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:
已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件: