��Ŀ����
2��ij�о���ѧϰС����̽�����ε���ֽ����ʱ����һ��ֱ�����ǰ��ֱ�Ƕ������ž���ABCD��AB��BC���ĶԽ��߽���O��ת����ͼ�١��ڡ��ۣ���ͼ��M��N�ֱ�Ϊֱ�����ǰ��ֱ�DZ������ABCD�ı�CD��BC�Ľ��㣮��1����ѧϰС����һ����Ա����ط��֣���ͼ�٣����ǰ��һֱ�DZ���OD�غϣ��У�BN2=CD2+CN2����ͼ�ۣ����ǰ��һֱ�DZ���OC�غϣ��У�BN��CN��CD֮��Ĺ�ϵCN2=CD2+BN2��
��2����̽��ͼ����BN��CN��CM��DM�������߶�֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�
��3����AB=8��BC=10���Ƿ����ijһ��תλ�ã�ʹ��CM+CN����$\frac{44}{5}$�������ڣ��������ʱDM�ij����������ڣ���˵�����ɣ�

���� ��1�����ı���ABCD�Ǿ��κ����ǰ���ص㣬�õ�OB=OD����DON=90�����ù��ɶ��������ɣ�
��2�����ı���ABCDΪ���κ����ǰ���ص㣬�ó����ۣ��жϳ���BON�ա�DOP�������ù��ɶ��������ɣ�
��3���ɾ��κ����ǰ���ص��Լ���ת�����ʵõ���MP=MN�����ù��ɶ�����Ȼ����CM+CN=$\frac{44}{5}$�����ɣ�
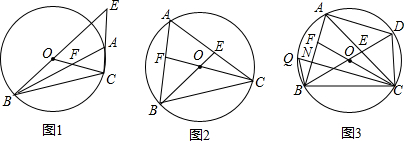
��� ��1��֤������ͼ�٣�����DN��
���ı���ABCD�Ǿ��Σ�
��OB=OD��
�ߡ�DON=90�㣬
��BN=DN��
�ߡ�BCD=90�㣬
��DN2=CD2+CN2��
��BN2=CD2+CN2��
��ͼ�ۣ�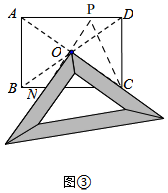
�ӳ�NO��AD��P��
���ı���ABCD�Ǿ��Σ�
��OD=OB��AD��BC��
���DPO=��BNO����PDO=��NBO��
�ڡ�BON�͡�DOP��
$\left\{\begin{array}{l}{��NBO=��PDO}\\{��BNO=��DPO}\\{OB=OD}\end{array}\right.$��
���BON�ա�DOP��
��ON=OP��BN=PD��
��OC��DP��
��CN=CP��
���ݹ��ɶ����ã�CP2=DP2+CD2��
��CN2=BN2+CD2
�ʴ�ΪCN2=CD2+BN2��
��2��֤������ͼ�ڣ��ӳ�NO��AD�ڵ�P������PM��MN��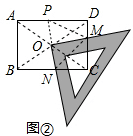
���ı���ABCD�Ǿ��Σ�
��OD=OB��AD��BC��
���DPO=��BNO����PDO=��NBO��
�ڡ�BON�͡�DOP��
$\left\{\begin{array}{l}{��NBO=��PDO}\\{��BNO=��DPO}\\{OB=OD}\end{array}\right.$��
���BON�ա�DOP��
��ON=OP��BN=PD��
�ߡ�MON=90�㣬
��PM=MN��
�ߡ�ADC=��BCD=90�㣬
��PM2=PD2+DM2��MN2=CM2+CN2��
��PD2+DM2=CM2+CN2��
��BN2+DM2=CM2+CN2��
��3����ͼ�ۣ�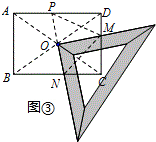
�ӳ�NO��AD�ڵ�P������MN��MP��
��OΪ����ABCD�ĶԽ��ߵĽ��㣬
������ת�ɵã�BN=DP��OP=ON��
��OM��ֱƽ��PN��
��MP=MN��
��Rt��MDP��MP2=DP2+DM2��
��Rt��MCN��MM2=CN2+CM2��
��MP=MN��BN=DP��
��BN2+DM2=CN2+CM2��
��DM=x��CN=y��
��CM=8-x��BN=10-y��
�ࣨ10-y��2+x2=y2+��8-x��2��
��y=$\frac{4}{5}$x+$\frac{9}{5}$��
��CM+CN=8-x+y=8-x+$\frac{4}{5}$x+$\frac{9}{5}$=$\frac{49}{5}$-$\frac{1}{5}$x��
��CM+CN=$\frac{44}{5}$��
��$\frac{49}{5}$-$\frac{1}{5}$x=$\frac{44}{5}$��
��x=5��
�൱DM=5ʱ��CM+CN=$\frac{44}{5}$��
���� �����Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ����ε����ʣ����ɶ������ù��ɶ����õ�PM2=PD2+DM2��MN2=CM2+CN2ת����BN2+DM2=CM2+CN2�ǽⱾ��Ĺؼ���

 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�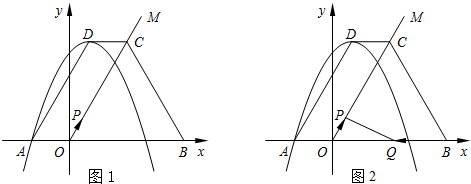
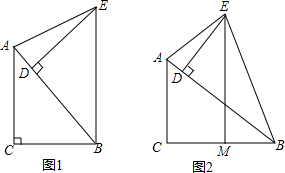
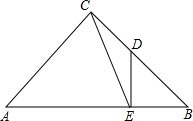 ��ͼ����֪��ABC�ǵ���ֱ�������Σ���ACB=90�㣬��BC���е�D��DE��AB��E������CE����sin��ACE=$\frac{3\sqrt{10}}{10}$��
��ͼ����֪��ABC�ǵ���ֱ�������Σ���ACB=90�㣬��BC���е�D��DE��AB��E������CE����sin��ACE=$\frac{3\sqrt{10}}{10}$��