题目内容
12.解不等式组:$\left\{\begin{array}{l}{x+1>2}\\{5+x≥3(x-1)}\end{array}\right.$.分析 利用不等式的性质,先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{x+1>2①}\\{5+x≥3(x-1)②}\end{array}\right.$,
由①式得x>1;
由②式得x≤4,
所以不等式组的解为1<x≤4.
点评 此题考查解不等式组;求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
2.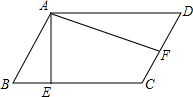 如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
 如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
7.已知∠α和∠β互为余角.若∠α=40°,则∠β等于( )
| A. | 40° | B. | 50° | C. | 60° | D. | 140° |
 已知:如图,四边形BCDE是矩形,AB=AC,求证:AE=AD.
已知:如图,四边形BCDE是矩形,AB=AC,求证:AE=AD. 如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.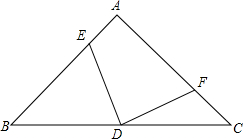 如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.
如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.