题目内容
3.(1)解方程组:$\left\{\begin{array}{l}{x-2y=1}\\{2x+2y=5}\end{array}\right.$(2)解方程:$\frac{2}{x+3}$=$\frac{1}{x}$.
分析 (1)方程组利用加减消元法求出解即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=1①}\\{2x+2y=5②}\end{array}\right.$,
①+②得:3x=6,即x=2,
把x=2代入①得:y=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$;
(2)去分母得:2x=x+3,
解得:x=3,
经检验x=3是分式方程的解.
点评 此题考查了解分式方程,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.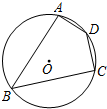 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
 如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.
如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.