题目内容
2.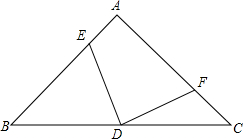 如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.
如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.
分析 根据等腰直角三角形的性质得到∠C=45°,中线AD平分∠BAC,并且AD=$\frac{1}{2}$BC,则∠BAD=∠C,AD=DC,又EA=CF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
解答 证明:连接AD,如图,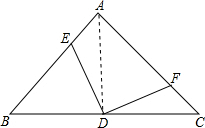
∵△ABC为等腰直角三角形,D为BC中点,
∴AD=DC,AD平分∠BAC,∠C=45°,
∴∠EAD=∠C=45°,
在△ADE和△CDF中
$\left\{\begin{array}{l}{EA=CF}\\{∠EAD=∠C}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF,
∴DE=DF,
∴∠ADE=∠CDF.
∵∠ADE+∠EDB=90°,
∴∠CDF+∠EDB=∠EDF=90°,即DE⊥DF.
点评 本题考查了全等三角形的判定与性质:如果两个三角形中有两组对应边相等,并且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等腰直角三角形性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若关于x的方程ax=3x-1的解是负数,则a的取值范围是( )
| A. | a<1 | B. | a>3 | C. | a>3或a<1 | D. | a<2 |
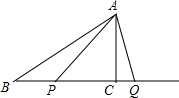 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.