题目内容
2.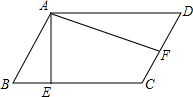 如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 设BC=3x,则CD=2x,由平行四边形的性质得出AB=CD=2x,AB∥DC,由已知条件得出∠BAF=90°,EC=2x,得出BE=$\frac{1}{2}$AB,证出∠BAE=30°,即可得出∠EAF的度数
解答 解:设BC=3x,则CD=2x,
∵四边形ABCD是平行四边形,
∴AB=CD=2x,AB∥DC,
∵AE⊥BC,AF⊥DC,
∴∠AEB=90°,AF⊥AB,
∴∠BAF=90°,
∵AB=EC,
∴EC=2x,
∴BE=BC=EC=x=$\frac{1}{2}$AB,
∴∠BAE=30°,
∴∠EAF=90°-30°=60°,
故选B.
点评 本题考查了平行四边形的性质、含30°角的直角三角形的判定、平行线的性质;熟练掌握平行四边形的性质,求出∠BAE=30°是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
10.一个多边形的每个内角均为120°,则这个多边形是( )
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
7.下列四种正多边形:①正三角形;②正方形;③正五边形;④正六边形,其中既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.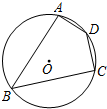 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
 如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.
如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.