题目内容
11.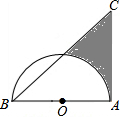 如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).
如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).
分析 连接OD,由OD=OB,∠CBA=45°可知OD⊥AB,即∠BOD=90°,再由S阴影=S△ABC-S扇形AOD-S△BOD即可得出结论.
解答  解:连接OD,
解:连接OD,
∵OD=OB,∠CBA=45°,AB=4,
∴OD⊥AB,即∠BOD=90°,
∴S阴影=S△ABC-S扇形AOD-S△BOD=$\frac{1}{2}$×4×4-$\frac{1}{4}$π×4-$\frac{1}{2}$×2×2=8-π-2
=6-π.
故答案为:6-π.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.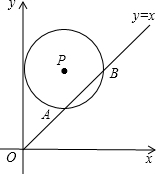 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
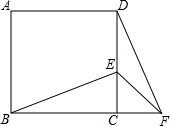 已知BC=CD,∠BCD=90°,CE=CF,图中有全等三角形吗?如果有,请证明.
已知BC=CD,∠BCD=90°,CE=CF,图中有全等三角形吗?如果有,请证明.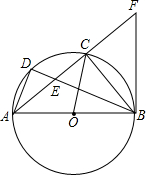 如图,在△ABC内接于⊙O,AB为直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$.
如图,在△ABC内接于⊙O,AB为直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$.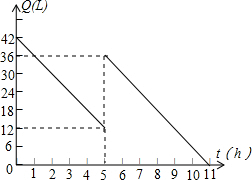 某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题: