题目内容
5.正方形的边长为10cm,在其中挖去一个边长为x cm的正方形(1)求x的取值范围;
(2)若剩余部分的面积为y cm2,写出y与x的函数解析式;
(3)当挖去的正方形的边长为1cm、2cm、3cm、$\sqrt{70}$cm时,求剩余部分的面积.
分析 (1)根据题意可知正方形的边长大于0,且小于10;
(2)剩余部分的面积=大正方形的面积-小正方形的面积;
(3)将x=1,2,3,$\sqrt{70}$分别代入y与x的函数关系式即可求得剩余部分的面积.
解答 解:(1)根据题意可知:0<x<10;
(2)y=10×10-x2=100-x2,
∴y与x的函数关系是为y=100-x2.
(3)将x=1代入得y=100-1=99;
所以剩余部分的面积为99平方厘米;
将x=2代入得y=100-4=96;
所以剩余部分的面积为96平方厘米;
将x=3代入得y=100-9=91;
所以剩余部分的面积为91平方厘米;
将x=$\sqrt{70}$代入得y=100-70=30;
所以剩余部分的面积为30平方厘米.
点评 本题主要考查的是二次函数的应用,根据题意列出函数关系式是解题的关键.

练习册系列答案
相关题目
16.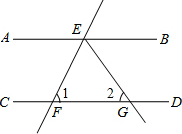 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )| A. | 70° | B. | 65° | C. | 55° | D. | 22.5° |
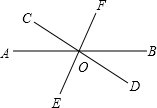 如图,直线AB、CD、EF相交于点O,∠AOC=35°,∠COF=80°.
如图,直线AB、CD、EF相交于点O,∠AOC=35°,∠COF=80°.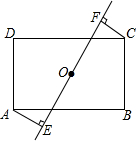 在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.
在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.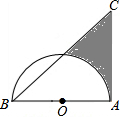 如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).
如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).