题目内容
1.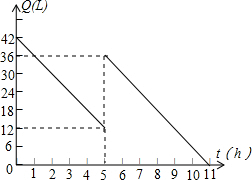 某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:(1)机动车行驶5h后加油,途中加油24升;
(2)根据图形计算,机动车在加油前的行驶中每小时耗油多少升?
(3)如果加油站距目的地还有400km,车速为60km/h,要到达目的地,油箱中的油是否够用?请说明理由.
分析 (1)图象上x=5时,对应着两个点,油量一多一少,可知此时加油多少;
(2)因为x=0时,Q=42,x=5时,Q=12,所以出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L;
(3)由图象知,加油后还可行驶6小时,即可行驶60×6千米,然后同400千米做比较,即可求出答案.
解答 解:(1)由图可得,机动车行驶5小时后加油为36-12=24;
(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,
因此每小时耗油量为6L,
(3)由图可知,加油后可行驶6h,
故加油后行驶60×6=360km,
∵400>360,
∴油箱中的油不够用.
点评 此题考查一次函数的实际应用,解答本题的关键是仔细观察图象,寻找题目中所给的信息,进而解决问题,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.解方程组$\left\{\begin{array}{l}{26x+29y=3,(1)}\\{29x+26y=-3,(2)}\end{array}\right.$,下列四种方法中,最简便的是( )
| A. | 代入消元法 | B. | (1)×29-(2)×26,先消去x | ||
| C. | (1)×26-(2)×29,先消去y | D. | (1)+(2),两方程相加 |
13.下列二次根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
10.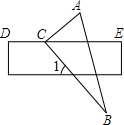 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )| A. | 135° | B. | 60° | C. | 50° | D. | 45° |
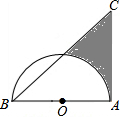 如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).
如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).