题目内容
20.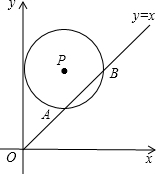 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,先根据切线的性质得PH=2,即⊙P的半径为2,再根据垂径定理,由PC⊥AB得到BC=CD=$\frac{1}{2}$AB=$\sqrt{3}$,接着在Rt△BPC中利用勾股定理可计算出PC=1,由直线y=x为第一、三象限的角平分线得到∠DOE=45°,则∠ODE=45°,DE=OE=2,然后判断△PCD为等腰直角三角形得到PD=$\sqrt{2}$PC=$\sqrt{2}$,所以PE=PD+DE=2+$\sqrt{2}$,即a=2+$\sqrt{2}$.
解答  解:作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,
解:作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,
∵⊙P与y轴相切,
∴PH=2,即⊙P的半径为2,
∵PC⊥AB,
∴BC=CD=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
在Rt△BPC中,PC=$\sqrt{P{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∵直线y=x为第一、三象限的角平分线,
∴∠DOE=45°,
∴∠ODE=45°,DE=OE=2,
∴∠PDC=45°,
∴PD=$\sqrt{2}$PC=$\sqrt{2}$,
∴PE=PD+DE=2+$\sqrt{2}$.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了坐标与图形性质、勾股定理和垂径定理.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10.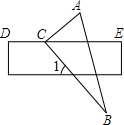 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )| A. | 135° | B. | 60° | C. | 50° | D. | 45° |
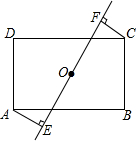 在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.
在矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线交点,过O作任意一条直线,分别过点A、C作直线l的垂线,垂足为E、F.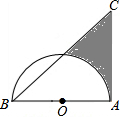 如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).
如图,在△ABC中,∠CAB=90°,∠CBA=45°,以AB为直径的半圆O,AB=4,则阴影部分面积为6-π(结果保留π).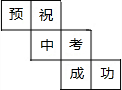 一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )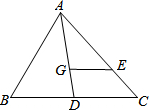 如图,点G为△ABC的重心,GE∥BC,BC=12,则GE=4.
如图,点G为△ABC的重心,GE∥BC,BC=12,则GE=4.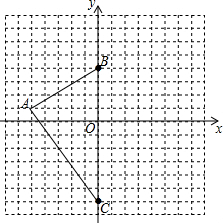 已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).
已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).