题目内容
14．化简（1）3b+5a-（2a-4b）
（2）5（3a2b-ab2）-4（-ab2+3a2b）；
（3）先化简，再求值：4（x-1）-2（x2+1）+$\frac{1}{2}$（4x2-2x），其中x=-3．
分析 （1）原式去括号合并即可得到结果；
（2）原式去括号合并即可得到结果；
（3）原式去括号合并得到最简结果，把x的值代入计算即可求出值．
解答 解：（1）原式=3b+5a-2a+4b=3a+7b；
（2）原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2；
（3）原式=4x-4-2x2-2+2x2-x=3x-6，
当x=-3时，原式=-15．
点评 此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠B=∠ACB=$\frac{1}{4}$∠BAC，CD是AB边上的高，CD=5，求BC的长．
9．
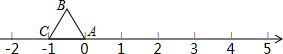等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1．若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2015次后，点B（ ）
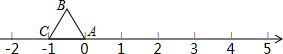等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1．若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2015次后，点B（ ）| A． | 不对应任何数 | B． | 对应的数是2013 | C． | 对应的数是2014 | D． | 对应的数是2015 |
如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，BD=5，则点D到BC的距离是（ ）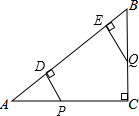
如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，P、Q是边AC、BC上的两个动点，PD⊥AB于点D，QE⊥AB于点E．设点P、Q运动的时间是t秒（t＞0）．若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回到点C停止运动；点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动，到达点C后停止运动，当t=2或4时，△APD和△QBE全等．
3．下列说法不正确的（ ）
| A． | 变量x，y满足x+3y=1，则y可以是x的函数 | |
| B． | 变量x，y满足y=x，则y是x的函数 | |
| C． | 变量x，y满足y2=x2，则y是x的函数 | |
| D． | 变量x，y满足y=x2，则y是x的函数 |
观察图中的三角形数阵，则第50行的最后一个数是1275．