题目内容
16. 如图,点E在AB上,∠CEB=∠B.∠ACD=∠ECB,∠D=∠A,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B.∠ACD=∠ECB,∠D=∠A,求证:CD=CA.
分析 如图,首先证明∠ACB=∠DCE,这是解决问题的关键性结论;然后运用AAS公理证明△ABC≌△DEC,即可解决问题.
解答 证明:∵∠B=∠CEB,
∴CE=CB,
∴∠ACB=∠ECB,
∴∠ACD+∠ACE=∠ECB+∠ACE,
即∠DCE=∠ACB,在△CAB与△CDE中,
$\left\{\begin{array}{l}{∠DCE=∠ACB}\\{∠D=∠A}\\{CE=CB}\end{array}\right.$,
∴△CAB≌△CDE(AAS),
∴CD=CA.
点评 该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是牢固掌握全等三角形的判定方法,这是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
5.(1)如表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程1,并将它的解填在表中的空白处.
(2)方程$\frac{x}{10}$-(x-a)=1的解是x=$\frac{70}{9}$,求a的值.该方程是否是(1)中所给出的一列方程中的一个方程?如果是,它是第几个方程?
| 序号 | 方程 | 方程的解 |
| 1 | $\frac{x}{4}$-(x-2)=1 | x=$\frac{4}{3}$ |
| 2 | $\frac{x}{5}$-(x-3)=1 | x=$\frac{10}{4}$ |
| 3 | $\frac{x}{6}$-(x-4)=1 | x=$\frac{18}{5}$ |
| … | … | … |
11.下列运算中结果正确的是( )
| A. | -3x+5x=-8x | B. | 5y-3y=2 | C. | 3x2y-2x2y=x2y | D. | 3a+2b=5ab |
1.如果一个三角形有两边长分别是3和5,那么第三边长可能是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
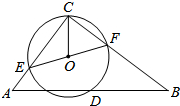 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,⊙O过C、D两点且分别交边AC、BC于点E、F,连接CO、EF.下列结论:
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,⊙O过C、D两点且分别交边AC、BC于点E、F,连接CO、EF.下列结论: