题目内容
1．如果一个三角形有两边长分别是3和5，那么第三边长可能是（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
分析 根据三角形的三边关系可得5-3＜x＜5+3，解不等式，确定x的取值范围，然后可得答案．
解答 解：设第三边长为x，由题意得：5-3＜x＜5+3，
即2＜x＜8，
故选：C．
点评 此题主要考查三角形的三边关系，要注意三角形形成的条件：任意两边之和大于第三边，三角形的两边差小于第三边．
练习册系列答案
活力课时同步练习册系列答案
相关题目
10．若9x2-12xy+m是两数和的平方式，那么m值是（ ）
| A． | 2y2 | B． | 4y2 | C． | ±4y2 | D． | ±16y2 |
9．
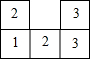一个几何体由大小相同的立方块搭成，从上面看到的如图所示，其中小正方形中的数字表示在该位置的立方块个数．若允许从该几何体中拿掉部分立方块，使剩下的几何体从正面和上面看的形状相同，则拿掉的立方块数量最多是（ ）
一个几何体由大小相同的立方块搭成，从上面看到的如图所示，其中小正方形中的数字表示在该位置的立方块个数．若允许从该几何体中拿掉部分立方块，使剩下的几何体从正面和上面看的形状相同，则拿掉的立方块数量最多是（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
如图，点E在AB上，∠CEB=∠B．∠ACD=∠ECB，∠D=∠A，求证：CD=CA．
如图，AE=AD，∠B=∠C，BE=4，AD=5，则AC=9．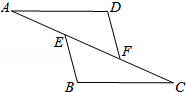
如图，已知点E，F在AC上，AD∥BC，DF=BE，添加的一个条件（不要在图中增加任何字母和线），使△ADF≌△CBE．你添加的条件是：∠D=∠B．
10．我们知道$\sqrt{10}$是一个无理数，那么$\sqrt{10}+1$在哪两个整数之间？（ ）
| A． | 1与2 | B． | 2与3 | C． | 3与4 | D． | 4与5 |
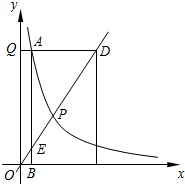如图，已知正比例函数的图象与反比例函数的图象都经过点P（2，3），点D是正比例函数图象上的一点，过点D作y轴的垂线，垂足分别Q，DQ交反比例函数的图象于点A，过点A作x轴的垂线，垂足为B，AB交正比例函数的图于点E．