题目内容
6．计算：$\sqrt{125}$+3$\sqrt{\frac{2}{27}}$-$\frac{1}{4}$$\sqrt{24}$+3$\sqrt{\frac{1}{5}}$．分析 先将二次根式化为最简，然后合并同类二次根式即可．
解答 解：原式=5$\sqrt{5}$+$\frac{\sqrt{6}}{3}$-$\frac{\sqrt{6}}{2}$+$\frac{3\sqrt{5}}{5}$
=$\frac{28\sqrt{5}}{5}$-$\frac{\sqrt{6}}{6}$．
点评 本题考查了二次根式的加减运算，解答本题的关键是掌握二次根式的化简及同类二次根式的合并．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，点E在AB上，∠CEB=∠B．∠ACD=∠ECB，∠D=∠A，求证：CD=CA．
17．有一个数值转换器，原理如图所示：
当输入的x=625时，输出的y等于（ ）
当输入的x=625时，输出的y等于（ ）
| A． | 25 | B． | 5 | C． | $\sqrt{2}$ | D． | $\sqrt{5}$ |
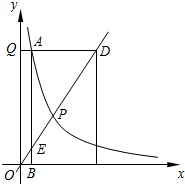如图，已知正比例函数的图象与反比例函数的图象都经过点P（2，3），点D是正比例函数图象上的一点，过点D作y轴的垂线，垂足分别Q，DQ交反比例函数的图象于点A，过点A作x轴的垂线，垂足为B，AB交正比例函数的图于点E．
16．已知|a|=5，|b|=2，|a-b|=b-a，则a+b的值是（ ）
| A． | -7 | B． | -3 | C． | -7或-3 | D． | 以上都不对 |