题目内容
4.化简:$\frac{8+2\sqrt{15}-\sqrt{10}-\sqrt{6}}{\sqrt{5}+\sqrt{3}-\sqrt{2}}$.分析 把分子的8分成5和3,则可把分子利用因式分解的方法变形,然后约分即可.
解答 解:原式=$\frac{5+\sqrt{15}-\sqrt{10}+\sqrt{15}+3-\sqrt{6}}{\sqrt{5}+\sqrt{3}-\sqrt{2}}$
=$\frac{\sqrt{5}(\sqrt{5}+\sqrt{3}-\sqrt{2})+\sqrt{3}(\sqrt{5}+\sqrt{3}-\sqrt{2})}{\sqrt{5}+\sqrt{3}-\sqrt{2}}$
=$\frac{(\sqrt{5}+\sqrt{3}-\sqrt{2})(\sqrt{5}+\sqrt{3})}{\sqrt{5}+\sqrt{3}-\sqrt{2}}$
=$\sqrt{5}$+$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
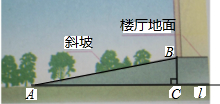 如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01).
如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01). 如图,点E在AB上,∠CEB=∠B.∠ACD=∠ECB,∠D=∠A,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B.∠ACD=∠ECB,∠D=∠A,求证:CD=CA.