题目内容
11.解不等式组$\left\{\begin{array}{l}{2-x≤0}\\{3(5x+1)>4x-8}\end{array}\right.$的解集为x≥2.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{2-x≤0…①}\\{3(5x+1)>4x-8…②}\end{array}\right.$,
解①得x≥2,
解②得x>-1.
则不等式组的解集是:x≥2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
2.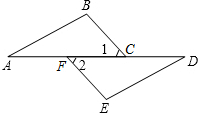 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )| A. | ∠E=∠B | B. | ED=BC | C. | AB=EF | D. | AF=CD |
6.一列单项式按以下规律排列:a,3a2,5a3,7a,9a2,11a3,13a,…,则第2016个单项式应是( )
| A. | 4031a3 | B. | 4031a | C. | 4031a2 | D. | 4032a3 |
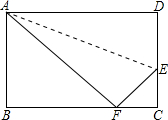 如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.