题目内容
6.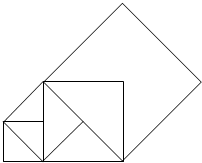 如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.
如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.
分析 第1个正方形的边长是1,对角线长为$\sqrt{2}$;第二个正方形的边长为$\sqrt{2}$,对角线长为($\sqrt{2}$)2=2,第3个正方形的对角线长为($\sqrt{2}$)3;得出规律,即可得出结果.
解答 解:第1个正方形的边长是1,对角线长为$\sqrt{2}$;
第二个正方形的边长为$\sqrt{2}$,对角线长为($\sqrt{2}$)2=2
第3个正方形的边长是2,对角线长为2$\sqrt{2}$=($\sqrt{2}$)3;…,
∴第n个正方形的对角线长为($\sqrt{2}$)n;
故答案为:($\sqrt{2}$)n.
点评 本题主要考查了正方形的性质、勾股定理;求出第一个、第二个、第三个正方形的对角线长,得出规律是解决问题的关键.

练习册系列答案
相关题目
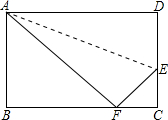 如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长. 如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.
如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.