题目内容
9.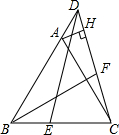 如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$.
如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$.
分析 连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=$\frac{1}{2}$=5.
解答 解:连接AF.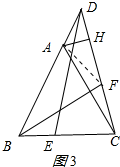
∵DE=DC,∠EDC=30°,
∴∠DEC=∠DCE=75°,
∴∠ACF=75°-60°=15°,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
在△ABF和△CBF中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
△ABF≌△CBF(SAS),
∴AF=CF,
∴∠FAC=∠ACF=15°,
∴∠AFH=15°+15°=30°,
∵AH⊥CD,
∴AH=$\frac{1}{2}$AF=$\frac{1}{2}$CF=$\frac{2}{3}$,
∵∠DEC=∠ABC+∠BDE,
∴∠BDE=75°-60°=15°,
∴∠ADH=15°+30°=45°,
∴∠DAH=∠ADH=45°,
∴DH=AH=$\frac{2}{3}$.
点评 本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键,注意辅助线的作法.

练习册系列答案
相关题目
4.把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
| A. | 1<m<7 | B. | 3<m<4 | C. | m>1 | D. | m<4 |
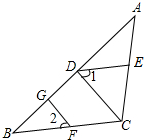 如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,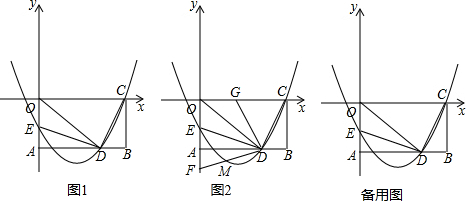
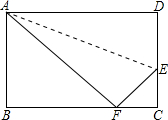 如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长. 如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.
如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.