题目内容
5.把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m可以取得的整数值有( )| A. | 1个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 直线y=-x-3向上平移m个单位后可得:y=-x-3+m,求出直线y=-x-3+m与直线y=2x+4的交点,再由此点在第二象限可得出m的取值范围.
解答 解:直线y=-x-3向上平移m个单位后可得:y=-x-3+m,
联立两直线解析式得:$\left\{\begin{array}{l}{y=-x-3+m}\\{y=2x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{m-7}{3}}\\{y=\frac{2m-2}{3}}\end{array}\right.$,
∵交点在第二象限,
∴$\left\{\begin{array}{l}{\frac{m-7}{3}<0}\\{\frac{2m-2}{3}>0}\end{array}\right.$,
解得:1<m<7.
m取整数有5个解.
故选D.
点评 本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第二象限的点的横坐标小于0、纵坐标大于0.

练习册系列答案
相关题目
10.某班5名同学在一次“1分钟仰卧起坐”测试中,成绩为(单位:次):38,44,42,38,39.这组数据的众数是( )
| A. | 40.2 | B. | 40 | C. | 39 | D. | 38 |
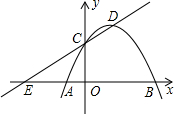 如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.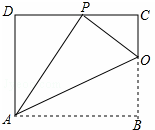 已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.
已知:如图,矩形ABCD的一条边AB=10,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕为AO.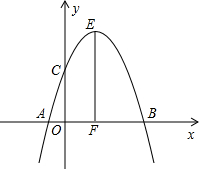 如图,抛物线y=-x2+2x+3经过点A、B、C,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,则实数m的变化范围为-$\frac{5}{4}$≤m≤5.
如图,抛物线y=-x2+2x+3经过点A、B、C,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,则实数m的变化范围为-$\frac{5}{4}$≤m≤5.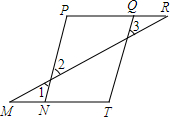 如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.
如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.