题目内容
在Rt△ABC中,AC=6,BC=8,∠C=90°,内切圆心为I,外接圆心为O,则OI= .
考点:三角形的内切圆与内心
专题:计算题
分析:作ID⊥AB于D,IE⊥AC于E,IF⊥BC于F,如图,先根据勾股定理计算出AB=10,根据直角三角形外心为斜边的中点得到AO=
AB=5,再证明四边形IECF为正方形,设⊙I的半径为r,则CF=CE=r,根据切线长定理得到BF=BD=8-r,AE=AD=6-r,所以8-r+6-r=10,解得r=2,则AD=4,OD=AO-AD=1,然后在Rt△IOD中利用勾股定理可计算出OI.
| 1 |
| 2 |
解答:解:作ID⊥AB于D,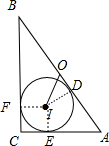 IE⊥AC于E,IF⊥BC于F,如图,
IE⊥AC于E,IF⊥BC于F,如图,
∵∠C=90°,AC=6,BC=8,
∴AB=
=10,
∵点O为△ABC的外心,
∴点O为斜边AB的中点,
∴AO=
AB=5,
∵∠C=90°,ID⊥AB,IE⊥AC,IF⊥BC,
而IF=IE,
∴四边形IECF为正方形,
设⊙I的半径为r,则CF=CE=r,
∴BF=BD=8-r,AE=AD=6-r,
∴8-r+6-r=10,解得r=2,
∴AD=6-2=4,
∴OD=AO-AD=1,
在Rt△IOD中,∵OD=1,ID=2,
∴OI=
=
.
故答案为
.
 IE⊥AC于E,IF⊥BC于F,如图,
IE⊥AC于E,IF⊥BC于F,如图,∵∠C=90°,AC=6,BC=8,
∴AB=
| AC2+BC2 |
∵点O为△ABC的外心,
∴点O为斜边AB的中点,
∴AO=
| 1 |
| 2 |
∵∠C=90°,ID⊥AB,IE⊥AC,IF⊥BC,
而IF=IE,
∴四边形IECF为正方形,
设⊙I的半径为r,则CF=CE=r,
∴BF=BD=8-r,AE=AD=6-r,
∴8-r+6-r=10,解得r=2,
∴AD=6-2=4,
∴OD=AO-AD=1,
在Rt△IOD中,∵OD=1,ID=2,
∴OI=
| OD2+ID2 |
| 5 |
故答案为
| 5 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了直角三角形的外心.

练习册系列答案
相关题目
等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角度数是( )
| A、65° | B、65°或25° |
| C、25° | D、50° |
数据1556000用科学记数法表示为( )
| A、1.556×107 |
| B、0.1556×108 |
| C、15.56×105 |
| D、1.556×106 |
 甲、乙两辆车分别从相距200km的A、B两地同时出发,他们离A地的路程随时间的变化的图象如图所示,则下列结论不正确的是( )
甲、乙两辆车分别从相距200km的A、B两地同时出发,他们离A地的路程随时间的变化的图象如图所示,则下列结论不正确的是( )| A、甲车的平均速度为40km/h | ||
| B、乙车行驶3h到达A地,稍作停留后离开A地 | ||
| C、乙车离开A地的平均速度比去A地的平均速度小 | ||
D、经
|
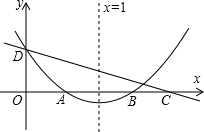 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A,B两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧),则下列命题中正确命题的个数是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A,B两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧),则下列命题中正确命题的个数是( )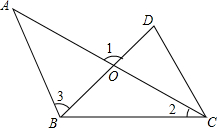 已知AB∥CD,AC平分∠BCD,∠2=35°,∠3=70°,求∠1的度数.
已知AB∥CD,AC平分∠BCD,∠2=35°,∠3=70°,求∠1的度数.