题目内容
等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角度数是( )
| A、65° | B、65°或25° |
| C、25° | D、50° |
考点:等腰三角形的性质
专题:
分析:分三角形为钝角三角形和锐角三角形两种情况,结合条件可求得顶角或顶角的外角,再结合三角形内角和定理可求得其底角.
解答:解:
当该三角形为锐角三角形时,如图1,

可求得其顶角为50°,
则底角为
×(180°-50°)=65°,
当该三角形为钝角三角形时,如图2,

可求得顶角的外角为50°,则顶角为130°,
则底角为
×(180°-130°)=25°,
综上可知该三角形的底角为65°或25°,
故选B.
当该三角形为锐角三角形时,如图1,

可求得其顶角为50°,
则底角为
| 1 |
| 2 |
当该三角形为钝角三角形时,如图2,

可求得顶角的外角为50°,则顶角为130°,
则底角为
| 1 |
| 2 |
综上可知该三角形的底角为65°或25°,
故选B.
点评:本题主要考查等腰三角形的性质和三角形内角和定理,掌握等边对等角和三角形内角和为180°是解题的关键.

练习册系列答案
相关题目
二次根式
有意义时,x的取值范围是( )
| x+3 |
| A、x≥-3 | B、x>-3 |
| C、x≤-3 | D、x≠-3 |
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
| A、10m | B、12m |
| C、15m | D、40m |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: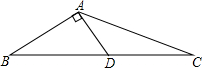 如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长.
如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长. 如图,已知△ABC和直线l,作出△ABC关于直线l的对称图形△A′B′C′.
如图,已知△ABC和直线l,作出△ABC关于直线l的对称图形△A′B′C′.