题目内容
8.若反比例函数$y=\frac{k}{x}$的图象经过点(1,4),则它的图象也一定经过的点是( )| A. | (-1,-4) | B. | (1,-4) | C. | (4,-1) | D. | (-1,4) |
分析 先根据已知点的坐标求得比例系数k的值,再根据图象上的点(x,y)的横纵坐标的积是定值4进行判断.
解答 解:∵反比例函数$y=\frac{k}{x}$的图象经过点(1,4),
∴k=1×4=4,
∴y=$\frac{4}{x}$,
∴函数图象上点的横、纵坐标的积是定值4,即xy=4,
∴(-1,-4)在函数图象上.
故选(A)
点评 本题主要考查了反比例函数图象上点的坐标特征,解题时注意:反比例函数y=$\frac{k}{x}$图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
19. 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长为( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长为( )
 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长为( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长为( )| A. | 13 | B. | 21 | C. | 18 | D. | 3 |
16.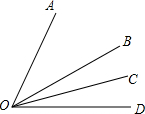 如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
 如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )| A. | 5° | B. | 10° | C. | 15° | D. | 20° |
3.直线l1:y=x+1与直线l2:y=mx+n的交点P的横坐标为1,则下列说法错误的是( )
| A. | 点P的坐标为(1,2) | |
| B. | 关于x、y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | |
| C. | 直线l1中,y随x的增大而减小 | |
| D. | 直线y=nx+m也经过点P |
13. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
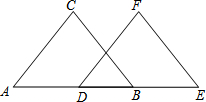 看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF
看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF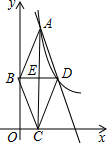 如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.
如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.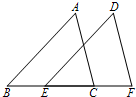 如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )
如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )