题目内容
19．
如图，在△ABC中，BC=5，AC=8，AB的垂直平分线交AB于点D，交AC于点E，则△BCE的周长为（ ）| A． | 13 | B． | 21 | C． | 18 | D． | 3 |
分析 根据线段垂直平分线的性质得到EA=EB，根据三角形的周长公式计算即可．
解答 解：∵DE是AB的垂直平分线，
∴EA=EB，
∴△BCE的周长=BC+CE+BE=BC+CE+EA=BC+AC=13，
故选：A．
点评 本题考查的是线段的垂直平分线的性质，线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
相关题目
10．
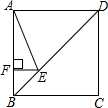如图，正方形ABCD的边长为8，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（ ）
如图，正方形ABCD的边长为8，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（ ）| A． | 2 | B． | 2$\sqrt{2}$ | C． | 8-4$\sqrt{2}$ | D． | 8$\sqrt{2}$-8 |
如图，已知AD∥BC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E，试说明AB∥DC，把下面的说理过程补充完整．
14．
如图，下列选项中，不能判断a∥b的是（ ）
如图，下列选项中，不能判断a∥b的是（ ）| A． | ∠1=∠3 | B． | ∠2=∠4 | C． | ∠2=∠3 | D． | ∠2+∠3=180° |
4．方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx+ay=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$，则a+b的值为（ ）
| A． | 1 | B． | -1 | C． | $\frac{5}{3}$ | D． | -3 |
8．若反比例函数$y=\frac{k}{x}$的图象经过点（1，4），则它的图象也一定经过的点是（ ）
| A． | （-1，-4） | B． | （1，-4） | C． | （4，-1） | D． | （-1，4） |
如图，在方格纸中每个小方格都是边长为1的正方形，A、B两点在小方格的顶点上，点C也在小方格的顶点上，且以A、B、C为顶点的三角形的面积为1个平方单位，则点C的个数为（ ）