题目内容
18.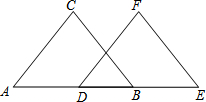 看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF
看图填空:已知,如图,BC∥EF,AD=BE,BC=EF.试说明△ABC≌△DEF解:∵AD=BE
∴AD+DB=BE+DB; 即:AB=DE
∵BC∥EF
∴∠ABC=∠E(两直线平行,同位角相等)
在△ABC和△DEF中,BC=EF,∠ABC=∠E,AB=DE,
∴△ABC≌△DEF (SAS).
分析 先根据等式的性质,得出AB=DE,再根据平行线的性质,得出∠ABC=∠E,最后根据SAS判定△ABC≌△DEF 即可.
解答 解:∵AD=BE,
∴AD+DB=BE+DB,即AB=DE,
∵BC∥EF,
∴∠ABC=∠E,(两直线平行,同位角相等)
在△ABC和△DEF中,BC=EF,∠ABC=∠E,AB=DE,
∴△ABC≌△DEF (SAS).
点评 本题主要考查了全等三角形的判定,解题时注意,两边及其夹角分别对应相等的两个三角形全等;两条平行线被第三条直线所截,同位角相等.

练习册系列答案
相关题目
13.能够成为直角三角形边长的三个正整数,我们称之为一组勾股数,观察表格所给出的三个数a,b,c,a<b<c.
(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
| 3,4,5 | 32+42=52 |
| 5,12,13, | 52+122=132 |
| 7,24,25 | 72+242=252 |
| 9,40,41 | 92+402=412 |
| … | … |
| 17,b,c | 172+b2=c2 |
10.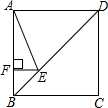 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 8$\sqrt{2}$-8 |
8.若反比例函数$y=\frac{k}{x}$的图象经过点(1,4),则它的图象也一定经过的点是( )
| A. | (-1,-4) | B. | (1,-4) | C. | (4,-1) | D. | (-1,4) |
 请在括号内加注理由或在横线上填入相关内容:
请在括号内加注理由或在横线上填入相关内容:



 如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.