题目内容
20.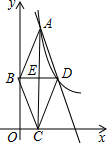 如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.
如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.(1)求点D的坐标(用含有m的代数式表示);
(2)判断四边形ABCD的形状,并说明理由;
(3)当m为何值时,四边形ABCD是正方形?并求出此时AD所在直线的解析式.
分析 (1)由点A在双曲线上,确定出A坐标,从而求出点E,D坐标;
(2)由(1)得到的点B,D,E的坐标判断出EB=ED,AE=EC,得出四边形ABCD是平行四边形,再用BD⊥AC即可;
(3)由(2)结合AC=BD建立方程求出m,从而得到点D,A坐标即可.
解答 解:(1)∵点A的横坐标为m,
∴点A的纵坐标为$\frac{8}{m}$,
∵E是AC的中点,AC⊥x轴,
∴E(m,$\frac{4}{m}$),
∵BD⊥AC,AC⊥x轴,
∴BD∥x轴,
∴点B,E,D的纵坐标相等,为$\frac{4}{m}$,
∴点D的横坐标为2m,
∴D(2m,$\frac{4}{m}$);
(2)四边形ABCD是菱形,
∵B(0,$\frac{4}{m}$),E(m,$\frac{4}{m}$),D(2m,$\frac{4}{m}$),
∴EB=ED=m,
∵AE=EC,
∴四边形ABCD是平行四边形,
∵BD⊥AC,
∴平行四边形ABCD是菱形;
(3)∵平行四边形ABCD是菱形,
∴当AC=BD时,四边形ABCD是正方形,
∴2m=$\frac{8}{m}$,
∴m=2,或m=-2(舍),
∴A(2,4),D(4,2),
设直线AD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=4}\\{4k+b=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴直线AD解析式为y=-x+6,
∴当m=2时,四边形ABCD是正方形,此时直线AD解析式为y=-x+6.
点评 此题是反比例函数综合题,主要考查了函数图象上的点的特点,平行四边形,菱形正方形的性质和判定,解本题的关键是用方程的思想解决问题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案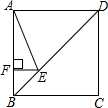 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 8$\sqrt{2}$-8 |
| A. | (-1,-4) | B. | (1,-4) | C. | (4,-1) | D. | (-1,4) |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,在方格纸中每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,点C也在小方格的顶点上,且以A、B、C为顶点的三角形的面积为1个平方单位,则点C的个数为( )
如图,在方格纸中每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,点C也在小方格的顶点上,且以A、B、C为顶点的三角形的面积为1个平方单位,则点C的个数为( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | 有两角和其中一角的对边对应相等的两个三角形全等 | |
| B. | 面积相等的两个三角形全等 | |
| C. | 有一边相等的两个等边三角形全等 | |
| D. | 三边对应相等的两个三角形全等 |
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$2\sqrt{2}$,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是2$\sqrt{3}$+2.