题目内容
10. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8.(1)求AB的长;
(2)把△ABC沿着直线AD翻折,使得点C落在AB边上E处,求折痕AD的长.
分析 (1)在Rt△ABC中利用勾股定理即可求出AB的长;
(2)首先根据折叠的性质可得∠C=∠AED=90°,AC=AE=6,CD=ED,则BE=4,设CD=DE=x,则DB=8-x,根据勾股定理得出DE2+EB2=DB2,即(8-x)2=42+x2,求出x=3.然后在Rt△ADC中利用勾股定理即可求出AD的长.
解答 解:(1)∵Rt△ABC中,∠C=90°,
∴AB2=AC2+BC2,
∵AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10; (2)根据折叠可得:∠C=∠AED=90°,AC=AE=6,CD=ED,则BE=4,
(2)根据折叠可得:∠C=∠AED=90°,AC=AE=6,CD=ED,则BE=4,
设CD=DE=x,则DB=8-x,
∵DE2+EB2=DB2,
∴(8-x)2=42+x2,
解得:x=3.
∵AD2=AC2+CD2,
∴AD=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$.
点评 该题主要考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理,牢固掌握翻折变换的性质是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
20.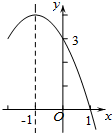 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
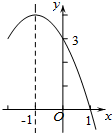 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-3 | D. | x1=1,x2=-4 |
1.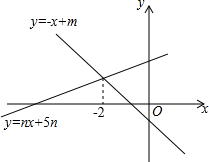 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )| A. | -5,-4,-3 | B. | -4,-3 | C. | -4,-3,-2 | D. | -3,-2 |
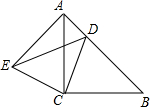 如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.
如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.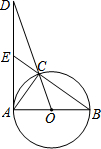 如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.