题目内容
18.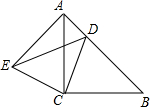 如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.
如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
分析 (1)根据∠ACB=∠ECD=90°求出∠DCB=∠ECA,根据SAS推出两三角形全等即可;
(2)根据等腰直角三角形求出∠BAC=∠B=45°,根据全等三角形的性质求出∠EAC=∠B=45°,求出∠EAD=90°,根据勾股定理求出即可.
解答 (1)证明:∵∠ACB=∠ECD=90°,
∴∠ACB-∠ACD=∠ECD-∠ACD,
∴∠DCB=∠ECA,
在△ACE和△BCD中
$\left\{\begin{array}{l}{CE=CD}\\{∠ACE=∠BCD}\\{CA=CB}\end{array}\right.$
∴△ACE≌△BCD(SAS);
(2)解:∵∠ACB=90°,AC=BC,
∴∠BAC=∠B=45°,
∵△ACE≌△BCD,
∴∠EAC=∠B=45°,
∴∠EAD=90°,
∴在Rt△AED中,∠EAD=90°,AE=3,AD=2,由勾股定理得:ED=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
点评 本题考查了等腰直角三角形,全等三角形的性质和判定,勾股定理的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
3.以3和4为根的一元二次方程是( )
| A. | x2-7x+12=0 | B. | x2+7x+12=0 | C. | x2+7x-12=0 | D. | x2-7x-12=0 |
 如图,在正方形网格中,每个小正方形的边长均为1,三角形ABC的三个顶点恰好落在格点上.
如图,在正方形网格中,每个小正方形的边长均为1,三角形ABC的三个顶点恰好落在格点上. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8. 如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.
如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.